行列式的值和特征值之间的关系_行列式的值与代数余子式的关系
行列式的值和特征值之间的关系。这种 *** 可以用来计算任意数量的函数,如果需要,还可以用来分析一些复杂的函数。在这里,我们将介绍一种简单的算法,它可以用来计算函数的整数部分。下面,我们将讨论如何使用这种 *** 。首先,我们需要知道什么是函数。
一:行列式的值和特征值之间的关系
特征值与行列式的关系为:特征值乘积等于对应方阵行列式的值,特征值的和等于对应方阵行列式对角线元素之和。矩阵A是方阵时,有行列式|A|,令|N-A|=0,解出特征值λ。一个特征空间就是一个由所有特征向量组成的空间有相同的特征值,包括零向量,特征值的几何多重性是对应特征空间的维数。
二:行列式的值怎么算
这就是一个《上三角》行列式,行列式=1*(-1)*(-1)*2005=2005
三:行列式的值与代数余子式的关系
特征值和特征向量具有良好的性质,是线性代数中的重要概念之一,在多元统计分析 *** 中也具有重要的应用。
在数学上,特别是线性代数中, A为n阶矩阵,若数λ和n维非0列向量v,满足Av=λv,那么数λ称为A的特征值,v称为A的对应于特征值λ的特征向量。
在多元统计中,特征值和特征向量主要在PCA主成分分析及FA因子分析中发挥作用。
在主成分分析中
特征向量正交化保证了主成分之间具有两两互不相关的性质单位化使主成分表达式中线性组合的系数更加简单;主成分的方差等于构成线性组合的特征向量相应的特征值,特征值的总和与原始变量的方差的总和相等,表示所有的主成分恰好反映了所有原始变量的全部信息特征值在选取主成分的过程中通过限定方差贡献程度,控制包含较多信息的主成分。
特征向量之间是正交的。
特征值的总和=矩阵R的迹(主对角线元素的总和)=总方差。
特征值的乘积=矩阵的行列式值=广义方差。
在因子分析中
特征值和特征向量用于对因子模型进行估计在对应分析中用于计算因子载荷矩阵。
进一步解释特征值/向量的作用,本文假设一个双变量模型。
给定相关系数矩阵R,从中得出2对特征值和特征向量。
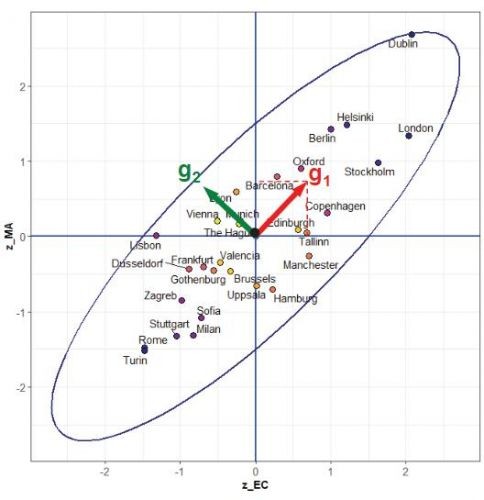
特征向量描述了这个椭圆的两条轴的方向。椭圆轴的半长和特征值的平方根是成比例的。所以,在2个变量时,特征值比较大的特征向量对应的就是长轴方向。因为这里只有2个维度,所以是一个平面图形。
原坐标系中,每个样本都对应了一个横纵坐标。现在,有了特征向量后,我们顺着特征向量的方向画两条新轴,也就是围绕椭圆建立新轴。因为轴心没有改变,所以每个样本与轴心的距离是不会改变的。改变的只有横纵坐标。
因为轴的顺序是按照特征值的大小排序的,所以在解释样本变异方向时,排序在前的轴重要性更高。
实例:
如下图,特征值总和都是2。但是每张图有不一样的特征值和特征向量。
左图:两个特征值很接近,因此椭圆的两条轴长度就相近。因此,样本的散落的位置接近于一个圆形。λ1稍微大一些,因此,红轴重要性稍微更高一些,我们可以推测可能存在一些负相关性,但也非常微小,接近于0,几乎不相关。
中间:λ1对应红轴,负方向。λ2对应绿轴,正方向。λ1>λ2,推断负相关是更加普遍的趋势,但是正相关也是存在的,所以这描述的是程度中等的负相关关系。
右图:λ1远大于λ2。说明红轴代表的正相关关系非常强烈,沿着绿轴可以发现,样本变异程度很小,因此推断,本样本间仍然以正相关关系为主。
四:行列式的值等于特征值的乘积
如果可对角化,那么答案是 等于 。重根有几个乘几次,它们各自对应了特征向量,一个也不能少。
是的,所有特征值之积,等于矩阵行列式;
而所有特征值之和,等于矩阵的迹